Albedo
Bypass Diodes
Solar Glazing
Single Phase Versus Three Phase Power Supply
Three phase power supply
Single Phase Power Supply
Module Measurement without Load
Module Measurement with Load
[...]
Effect of Temperature
Effect of Temperature on Solar cells
Solar cells are sensitive to temperature changes. An increase in temperature reduces the band gap of the semiconductor, thus affecting most of the parameters of semiconductor material. The decrease in the band gap of a semiconductor with increase in temperature is an increase in the energy of electrons in the material. Lower energy is thus required for breaking the bond. In a bond model of a band gap of a semiconductor, reducing the bond energy reduces also the band gap. Thus increasing the temperature also reduces the band gap. In the solar cell, the most affected parameter by temperature increase is the open circuit voltage. The open circuit voltage decreases with temperature decrease because of the temperature dependence of I0. The I0 equation from one side of a pn junction is:
where:
q: electronic charge
A: area
D: diffusivity of minority carrier provided for silicon as a function of doping
L: minority carrier diffusion length
ND: doping
ni: intrinsic carrier concentration
In the equation above, several parameters have temperature dependence, but the utmost important effect is due to ni ,intrinsic carrier concentration. ni depends on the band gap energy (where lower band gaps give a higher intrinsic carrier concentration), and on the energy that the carriers have (where higher temperatures give higher intrinsic carrier concentrations). The intrinsic carrier concentration equation is: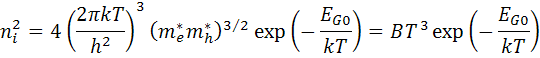
where:
T: temperature;
h & k: constants
me & mh : effective electrons and holes masses respectively;
EGO: band gap linearly extrapolated to absolute zero
B: constant independent of temperature.
Substituting the equations into the equation for I0, with assumption that the temperature dependencies of the other parameters is negligible;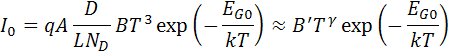
Where:
B': temperature independent constant
γ: A constant used instead of the number 3 to incorporate possible dependencies of temperature of other material parameters
The effect of I0 on open circuit voltage can be determined by the substitution of the equation of I0 into the Voc equation as below:
As EG0 = qVG0. Assuming dVoc/dT is independ on dIsc/dT, dVoc/dT can be determined as;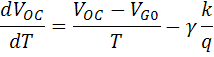
The equation above displays that temperature sensitivity for a solar cell is dependent on open circuit voltage of the solar cell, where the higher voltage solar cells are less affected by temperature. For silicon, EG0 value is 1.2, and using γ equal to 3 gives a reduction in the open circuit voltage of around 2.2 mV/°C;
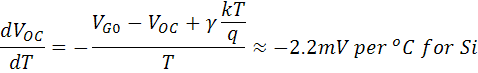The short circuit current, Isc, slightly increases with temperature, as band gap energy, EG, decreases and extra photons have enough energy for creating electron hole pairs. Yet, this effect is small.
jimmie
on 04 Nov 2022